
How much of the math you do in your classroom is based on someone else’s questions? Someone far away from your classroom? Someone other than your students? Even with specter of standardized tests looming like dark, heavy clouds, how can we leave room for the most important part of learning: question asking?
“So many of the things that we do in math education — and maybe more generally in education — are giving students answers to questions that they would never think of asking. By definition, that’s what it is to be boring. If you’re sitting at a bar and someone’s telling you stuff that you’re not interested in and you would never think of asking about — what is more boring than that? That seems to be the model of our educational system: ‘Here’s the formula for the cosine of the double angle.’ ‘Well, I don’t care about that.'” —Steven Strogatz
The first time I experimented with building scaled-up geometric forms I was homeschooling my then-seven-year-old. At the time she was a “resistant” learner which basically meant she was happiest exploring her own questions, and, over a couple years of homeschooling I realized my best strategy was to influence the child by way of my own curiosities and the way I structured the environment, leaving out provocations to be discovered and, if of interest, investigated. This was also a time when I was deep into finding answers for my own question “What is math?” and I was heavy into an investigation into Platonic Solids. I had never been a builder as a child, but I had a question and it needed to be answered.
Yesterday, on Twitter, I had a conversation with a third grade teacher who is reading Math on the Move and who has been wondering about how how to “scale up” her students’ mathematical activity. Specifically she’s been curious about my recent work with building body-scale polyhedra. Body- or moving-scale means that the whole body/person is engaged in problem solving and mathematical thinking to investigate a mathematical challenge or project of some kind. I think Telanna’s question could be anybody’s question who is wondering how we can do math off the page.
My answer focused on how I structure a making activity and the learning environment in a way that motivates learners to collaborate and ask new questions in response to the activity in an intrinsic way.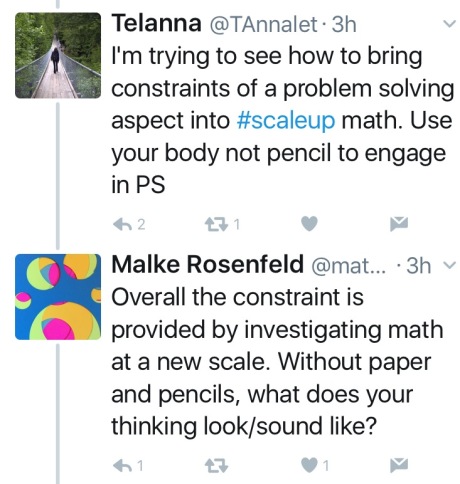









It’s in the process of making something with the freedom to try things out and see where it gets you that creates new questions.
It’s these questions, arising in the moments when they’re needed, born of collaboration, that help learners notice structure and pattern and purpose in what they’re doing. From there we can move to the more formal learning. But, like my daughter, I think kids in general are most motivated when they are provided agency by the adults in their lives. Their work may not be technically perfect, but they are in the best part of learning (to me, anyhow): inside the flow of an investigation filled with their wonderings.

To bring kids to math we need to leave room for their own questions.
What happens next? There are more questions to be asked about this kind of approach. I have my answers and am happy to share them. But I’d love to hear your questions first!






I am brimming with questions, but I feel like they are going to come off as a “give me the instructions for how to do this” when I think what I’d really like is to sit and watch and enjoy and understand this take place. Let me state that I am a-ok with open-ended problems and play. Having said that I’ll narrow down to 2 questions…
1) Could you say more about this:
“…the way I structured the environment, leaving out provocations to be discovered and, if of interest, investigated”
2) For the #miyfeet blue taped squares I can see how saying “what can you do and not do within this space?” and letting them go off to the races could wind up with kids jumping inside of them. As for building structures, was there any sort of question that led to their constructions?
Thanks!
LikeLike
Thanks for your questions! Here are my thoughts:
1. In homeschooling circles (which we were in for about two years) there’s a concept known as “strewing” which is really just a weird way of saying that you’re leaving out cool objects or books or whatever to be discovered by children if they happen upon it. For example, I used to leave magnetic puzzles on the fridge, an interesting book on the step in the living room, etc. Sometimes I’d simply do my own math art investigations which my daughter would join in her own way. If you’re interested I can share some examples from my old blog of what that looked like. I hold a very strong opinion that parallel play between adults and children is beneficial to both parties!
2. The blue tape squares ARE the constraints. There is also an inventory of “movement variables”, which are essentially pattern properties — 3 categories, movement, foot position, and type of movement, all based on my experience with percussive dance. The questions arise in the context of collaborating on math/dance making with a partner. Lots of conversations.
I guess you could say that as I design math/art activities I’m always thinking very closely about how to set up the environment, project, and materials in a way that allows for student agency. I think the method that most closely aligns with my approach to math & art is the Reggio approach which includes the environment as the “third teacher.” The other two, I think, are peers and the teacher.
Let me know if you have other questions!!
LikeLike
“Strewing”, I like that. In fact I’m nodding my head in agreement as I read all of your reply, especially “I’m always thinking very closely about how to set up the environment, project, and materials in a way that allows for student agency.”
I would really, really like to see examples from the old blog about parallel investigations with your daughter. Thanks!
LikeLike
Not sure if this will go with your comment that starts with a remark about strewing, but here you go with a parallel investigation I had with my 7yo about five years ago. Here are the blog posts in order:
http://mathinyourfeet.blogspot.com/2012/08/starting-stars-hexagondodecagon-edition.html
http://mathinyourfeet.blogspot.com/2012/08/seeing-stars.html
http://mathinyourfeet.blogspot.com/2012/08/plant-star-seeds-watch-them-grow.html
http://mathinyourfeet.blogspot.com/2012/09/joint-ventures-spinning-stars.html
http://mathinyourfeet.blogspot.com/2012/12/mathematical-star-ornaments.html
It was fun to relive those memories!!
LikeLike
Thank you for the post, Malke!
I think while I try to embrace developing the questions together with students in my practice, I sometimes forget that if I find a question that excites me, it doesn’t mean that it has the same value, intellectual and emotional, for my students. I can really relate to your thought, “To bring kids to math we need to leave room for their own questions.”
But here come some of my questions…
When I plan my lessons, I always keep in mind Daniel Willingham’s quote, “Memory is the residue of thought.” I want my students to build the context for mathematical concepts but I also need to support them in “mathematizing” this context, in thinking about mathematical aspects of their experience. How do I ensure that I support my students in noticing and wondering about mathematical concepts and structures in their explorations? How do I promote productive mathematical discussion and exchange of ideas without more focused common question?
LikeLike
I am so happy to continue our conversation from the other day! Here are some thoughts:
1. One way to mathematize an off-the-page activity like this is to bring it back down to the page by recording and/or reflecting on the process. In Math in Your Feet learners are asked to “map” their dance pattern. This activity is focused on integrating the information in a way that communicates the pattern in a different modality. Moving between modes of mathematical expression requires continual comparison between the two. And, it also requires precise thought to make sure that someone who doesn’t know your pattern can reproduce it from the map you’ve created. It’s a little different in the scaled-up making environment like the newspaper polyhedra here (and, I should say that this particular activity is still in its infancy and not yet fully conceptualized.)
2. Your comment reminded me about intuition in mathematics. In Tracy Zager’s new book (https://www.stenhouse.com/content/becoming-math-teacher-you-wish-youd-had) she quotes Erich Wittmann which I think mirrors some of what I was trying to express in this post:
“Intuitive experiences must be acquired by the student through his/her own activities–they cannot be learned through verbal instructions.”
3. Cognition arises from the spatial intuition we develop from living in and moving through the world. Whole body activity itself provides opportunities to develop intuition that might not be immediately verbal or even obvious at other scales and/or on the page. I am an advocate for language used in context, especially mathematics which has so much terminology. But I think mathematical intuition is inherently nonverbal, most likely the result of a lifetime of experiences reasoning spatially. I just went to Tracy Zager’s chapter on intuition and think (if you haven’t yet) you’d really like page 224-226 where she lays out the progression of questions to ask students s they’re moving toward understanding.
LikeLike
I am clearly not Malke but I see both your questions and Malke’s reply in our pal Simon Gregg’s classroom. The answer I have surmised from watching him this year is, think long-term.
At the beginning of the year his students were playing with cuisenaire rods, just making random faces and such. That slowly morphed into hundred faces, then comparisons, and next thing you know the students are recording deep mathematical reasoning on paper from their play. All three of Malke’s points in her reply have been prevalent throughout the development of Simon’s students. Sure, he’s teaching kindergarten, but these ideas seem like they scale up or down the grade continuum.
LikeLiked by 1 person
Thank you, it makes sense. Thinking more about learning trajectories rather than disconnected learning experiences. I think I am panicking a bit at the end of the year with the sense that the time is running out. I just need to be reminding myself that rushing through means students will need many more revisions and I might end up further behind.
LikeLike
I love the idea of the newspaper rolls but haven’t tried those yet.
I do a polygon charades game sometimes with a large loop of rope. Group of five or so students, bunch of polygon names in a hat. (Or two teams where they make clues for each other.) One person pulls a paper slip, then positions the rest of the people on the rope until they guess the shape. No words. Very fun. The nature of the game pushes specific names.
LikeLiked by 1 person